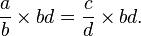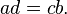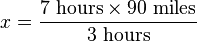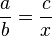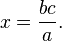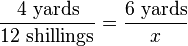GED Lesson: Ratio and Proportions (Cross Multiplying)

Click here for practice problems

Cross-multiplication

From Wikipedia, the free encyclopedia

  (Redirected from Cross multiplying)

In mathematics, specifically in elementary arithmetic and elementary algebra, given an equation between two fractions or rational expressions, one can cross-multiply to simplify the equation or determine the value of a variable.

Given an equation like:

(where b and d are not zero), one can cross-multiply to get:

In Euclidean geometry the same calculation can be achieved by considering the ratios as those of similar triangles.

Contents

  [hide] 

• 1Procedure
• 2Use
• 3Rule of Three
• 4References
• 5Further reading

Procedure[edit]

In practice, the method of cross-multiplying means that we multiply the numerator of each (or one) side by the denominator of the other side, effectively crossing the terms over.

The mathematical justification for the method is from the following longer mathematical procedure. If we start with the basic equation:

we can multiply the terms on each side by the same number and the terms will remain equal. Therefore, if we multiply the fraction on each side by the product of the denominators of both sides—bd—we get:

We can reduce the fractions to lowest terms by noting that the two occurrences of  on the left-hand side cancel, as do the two occurrences of d on the right-hand side, leaving:

and we can divide both sides of the equation by any of the elements—in this case we will use d—getting:

Another justification of cross-multiplication is as follows. Starting with the given equation:

multiply by d/d = 1 on the left and by b/b = 1 on the right, getting:

and so:

Cancel the common denominator bd = db, leaving:

Each step in these procedures is based on a single, fundamental property of equations. Cross-multiplication is a shortcut, an easily understandable procedure that can be taught to students.

Use[edit]

This is a common procedure in mathematics, used to reduce fractions or calculate a value for a given variable in a fraction. If we have an equation like this, where x is a variable we are interested in solving for:

we can use cross multiplication to determine that:

SAMPLE PROBLEM

For example, let's say that we want to know how far a car will get in 7 hours, if we happen to know that its speed is constant and that it already travelled 90 miles in the last 3 hours. Converting the word problem into ratios we get

Cross-multiplying yields:

and so:

Note that even simple equations like this:

are solved using cross multiplication, since the missing b term is implicitly equal to 1:

Any equation containing fractions or rational expressions can be simplified by multiplying both sides by the least common denominator. This step is called clearing fractions.

Rule of Three[edit]

The Rule of Three^[1] is a shorthand version for a particular form of cross-multiplication, that may be taught to students by rote. It figures in the French national curriculum for secondary education.^[2]

For an equation of the form:

where the variable to be evaluated is in the right-hand denominator, the Rule of Three states that:

and then using cross-multiplication to calculate x:

Click here for practice problems

GED LESSON: Mindset and Math

FULL EDWEEK ARTICLE

"Having a positive mindset in math may do more than just help students feel more confident about their skills and more willing to keep trying when they fail; it may prime their brains to think better.

In an ongoing series of experiments at Stanford University, neuroscientists have found more efficient brain activity during math thinking in students with a positive mindset about math.

It's part of a growing effort to map the biological underpinnings of what educators call a positive or growth mindset, in which a student believes intelligence or other skills can be improved with training and practice, rather than being fixed and inherent traits.

"Our findings provide strong evidence that a positive mindset contributes to children's math competence," said Lang Chen, a Stanford University postdoctoral fellow in cognitive psychology and neuroscience. "Beyond the emotional or even motivational story of 'positive mindset,' there may be cognitive functions supporting the story."